Introduction to Quantum Hall Effect
The Quantum Hall Effect (QHE) is a phenomenon observed in two-dimensional electron systems, where the Hall conductance exhibits quantized plateaus at integer multiples of the fundamental conductance quantum. This effect was first discovered in 1980 by Klaus von Klitzing, who was awarded the Nobel Prize in Physics for his discovery. The QHE has since become a fundamental concept in condensed matter physics, with far-reaching implications for our understanding of quantum mechanics and its applications in materials science and technology.
What is Quantization of Hall Conductance?
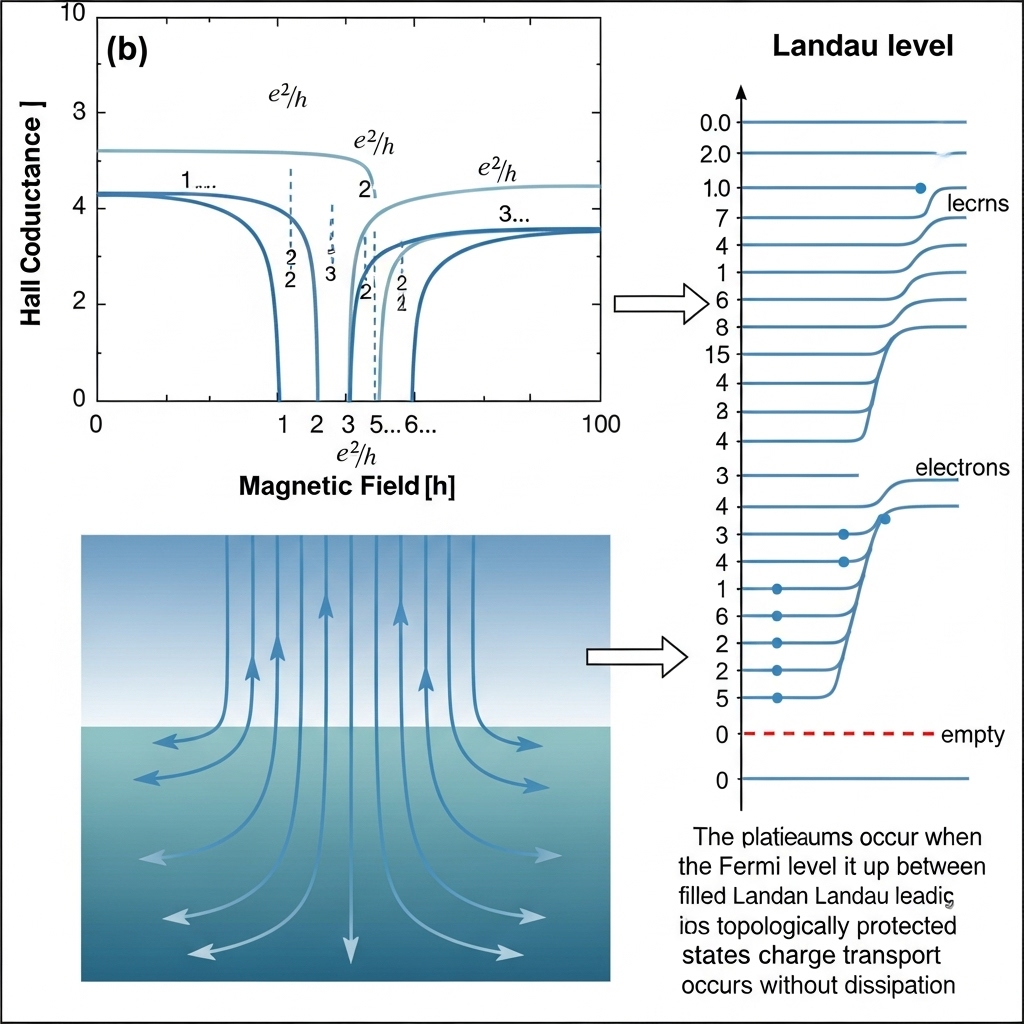
Quantization of Hall conductance refers to the phenomenon where the Hall conductance of a two-dimensional electron system exhibits discrete, step-like behavior as a function of the applied magnetic field. The Hall conductance is defined as the ratio of the Hall current to the applied voltage, and it is typically measured in units of e^2/h, where e is the elementary charge and h is the Planck constant. The quantization of Hall conductance is characterized by the formation of plateaus in the Hall conductance curve, where the conductance remains constant over a range of magnetic field values.
The Role of Landau Levels in QHE
The quantization of Hall conductance in QHE can be understood in terms of the formation of Landau levels in the two-dimensional electron system. In the presence of a strong magnetic field, the energy levels of the electrons in the system become quantized, forming a set of discrete energy levels known as Landau levels. The energy separation between adjacent Landau levels is given by the cyclotron energy, which is proportional to the magnetic field strength. As the magnetic field is increased, the Landau levels move to higher energies, and the Fermi level crosses each Landau level in turn, resulting in a step-like behavior in the Hall conductance.
Edge States and Quantum Hall Effect
Another key concept in understanding the QHE is the role of edge states in the two-dimensional electron system. Edge states are localized states that exist at the boundary of the system, and they play a crucial role in the transport of electrons in the QHE regime. The edge states are responsible for the dissipationless transport of electrons, which is a hallmark of the QHE. The edge states are also responsible for the formation of the quantized Hall plateaus, as they provide a mechanism for the electrons to move from one Landau level to the next.
Experimental Evidence for QHE
The QHE has been extensively studied experimentally, and a wide range of measurements have confirmed the quantization of Hall conductance. One of the most striking examples of the QHE is the measurement of the Hall conductance in a two-dimensional electron gas (2DEG) in a semiconductor heterostructure. The Hall conductance is measured as a function of the magnetic field, and the resulting curve exhibits a series of quantized plateaus, with each plateau corresponding to a specific integer multiple of the fundamental conductance quantum. The QHE has also been observed in other systems, including graphene and topological insulators.
Theoretical Models of QHE
A number of theoretical models have been developed to explain the QHE, including the integer quantum Hall effect (IQHE) and the fractional quantum Hall effect (FQHE). The IQHE is characterized by the formation of quantized Hall plateaus at integer multiples of the fundamental conductance quantum, and it is well described by the single-particle picture of non-interacting electrons. The FQHE, on the other hand, is characterized by the formation of quantized Hall plateaus at fractional multiples of the fundamental conductance quantum, and it is thought to arise from the interaction between electrons in the system. Theoretical models of the QHE have been highly successful in explaining the experimental data, and they have provided a deep understanding of the underlying physics of the effect.
Conclusion
In conclusion, the quantization of Hall conductance in the Quantum Hall Effect is a fascinating phenomenon that has been the subject of intense research in condensed matter physics. The QHE is characterized by the formation of quantized Hall plateaus, which arise from the interplay between the Landau levels, edge states, and electron-electron interactions in the two-dimensional electron system. The QHE has been extensively studied experimentally and theoretically, and it has far-reaching implications for our understanding of quantum mechanics and its applications in materials science and technology. Further research on the QHE is likely to continue to reveal new and exciting phenomena, and to provide a deeper understanding of the underlying physics of this complex and fascinating effect.
