Introduction to Lines and Curves
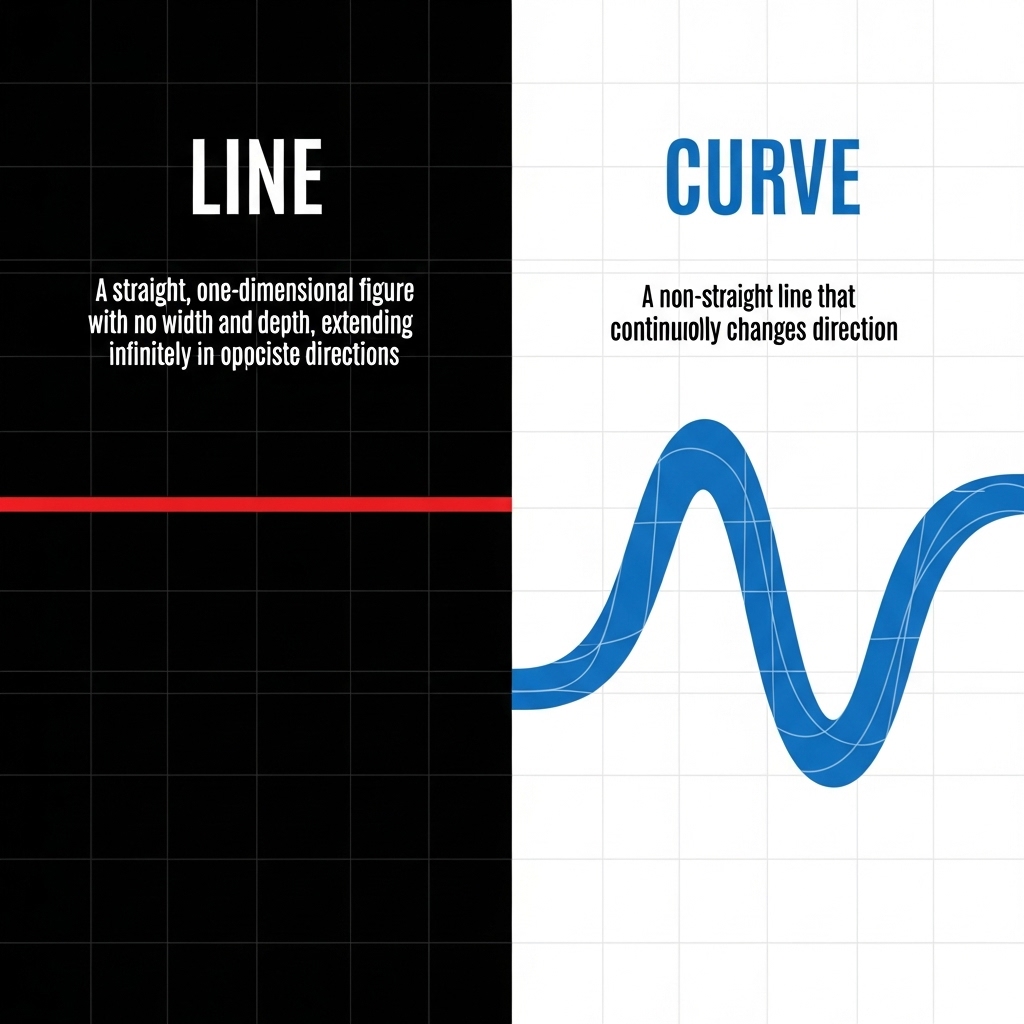
In the realm of geometry, two fundamental concepts are often discussed: lines and curves. These terms are used to describe different types of geometric shapes and are essential in understanding various mathematical and real-world phenomena. A line is a set of points that extend infinitely in two directions, while a curve is a continuous, smooth shape that can be open or closed. In this article, we will delve into the differences between lines and curves, exploring their definitions, properties, and applications.
Definition of a Line
A line is a set of points that extend infinitely in two directions, with no thickness or curvature. It is defined by two distinct points and can be represented graphically using the equation of a line, which is typically in the form y = mx + b, where m is the slope and b is the y-intercept. Lines can be classified into different types, including horizontal, vertical, and diagonal lines. For example, the equation y = 2x + 3 represents a line with a slope of 2 and a y-intercept of 3.
Definition of a Curve
A curve, on the other hand, is a continuous, smooth shape that can be open or closed. It can be thought of as a line that has been bent or curved in some way. Curves can be classified into different types, including circles, ellipses, parabolas, and hyperbolas. Unlike lines, curves do not have a constant slope and can change direction at any point. For instance, the equation x^2 + y^2 = 4 represents a circle with a radius of 2, centered at the origin.
Key Differences Between Lines and Curves
One of the primary differences between lines and curves is their shape. Lines are straight and extend infinitely in two directions, while curves are continuous and smooth, with no sharp corners or edges. Another significant difference is the slope. Lines have a constant slope, while curves have a varying slope that changes at every point. Additionally, lines are typically defined by two points, while curves are defined by a set of points that satisfy a specific equation. For example, the curve y = x^2 is defined by the set of points (x, y) that satisfy the equation, whereas the line y = 2x is defined by the two points (0, 0) and (1, 2).
Applications of Lines and Curves
Both lines and curves have numerous applications in various fields, including physics, engineering, architecture, and computer graphics. Lines are used to represent the path of an object, the trajectory of a projectile, or the boundary of a shape. Curves, on the other hand, are used to model real-world phenomena, such as the trajectory of a ball, the shape of a bridge, or the design of a car. For instance, the curve of a parabola can be used to model the trajectory of a projectile under the influence of gravity, while the line of a horizon can be used to represent the boundary between the earth and the sky.
Real-World Examples of Lines and Curves
In real-world scenarios, lines and curves are omnipresent. For example, the path of a road is typically a line, while the shape of a coin is a curve. The trajectory of a thrown ball is a curve, while the boundary of a building is a line. The design of a car's body is a combination of lines and curves, with the hood and trunk forming a curve, while the side panels form a line. Even in nature, lines and curves are abundant, with the shape of a leaf, the path of a river, and the trajectory of a bird in flight all exhibiting characteristics of lines and curves.
Conclusion
In conclusion, the difference between a line and a curve in geometry is significant, with distinct definitions, properties, and applications. While lines are straight and extend infinitely in two directions, curves are continuous and smooth, with no sharp corners or edges. Understanding the differences between lines and curves is essential in various fields, including physics, engineering, architecture, and computer graphics. By recognizing and applying the concepts of lines and curves, we can better model and analyze real-world phenomena, leading to innovative solutions and discoveries. Whether it's the design of a car, the trajectory of a projectile, or the shape of a bridge, the distinction between lines and curves plays a vital role in shaping our understanding of the world around us.
